Strijd tussen realistisch en traditioneel rekenen
De methode van directe instructie is weer terug. Na een periode van ‘ontdekkend leren’, waarbij de leraar slechts coach is, mag de leraar nu weer eerst zelf vertellen, waarna de leerling met de opgedane kennis verder kan.
Volgens de cognitieve psychologie heeft een leerling kennis nodig om een probleem overzichtelijk te maken. „Het kortetermijngeheugen is maar beperkt. Als een leerling zonder voorkennis een probleem moet oplossen, raakt dat geheugen overbelast”, zegt Paul Kirschner, universiteitshoogleraar in de onderwijspsychologie aan de Open Universiteit. Daarnaast raakt een leerling volgens hem gemotiveerd als die door herhaalde oefening het gevoel krijgt de stof te beheersen. De leraar moet dan meer zijn dan alleen coach.
Het oefenen, in hedendaags jargon ‘automatiseren’, was er sinds de jaren negentig op veel scholen bij ingeschoten. Nu is er op veel scholen sprake van een terugkeer naar vormen van klassikale instructie. Wetenschappelijk onderzoek stuurt deze trend.
Hattie deelt in het boek Leren zichtbaar maken bewezen leermethoden in naar rangorde van effectiviteit. „We moeten veel herhalen voor we meer complexe taken kunnen leren. Dit is een belangrijke reden waarom we expliciete instructie nodig hebben”, schrijft hij. Een goede leraar moet volgens hem expertise hebben in „veelvuldige” leerstrategieën die zich hebben bewezen. Directe feedback bijvoorbeeld.
Realistisch rekenen
Veel van deze technieken zijn voor de leraren nieuw. Zij hebben behoefte aan houvast omdat in het rekenen veel is veranderd. Zo werd vanaf eind vorige eeuw het realistisch rekenen ingevoerd: om inzicht te krijgen moeten kinderen dan zelf een oplossingsstrategie bedenken. Hoe zou je 2.056 door 28 delen? Leerlingen krijgen dan geen staartdeling maar moeten zelf eerst over stappen nadenken.
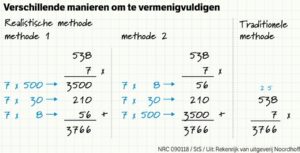
Deze methode werd vanaf de jaren zeventig ontwikkeld door het Freudenthal Instituut van de Universiteit Utrecht, voor het bèta-onderwijs. Hoewel dat niet de bedoeling was, leerden op veel scholen de leerlingen de tafels van vermenigvuldiging niet meer van buiten. Door een eigen rekenstrategie kunnen ze die omzeilen. In plaats van de uitkomst van zes maal acht automatisch op te dreunen kun je een tussenstap nemen door eerst vijf maal acht te nemen en daar dan nog een keer acht bij op te tellen. Zo’n tussenstap biedt rekeninzicht maar kost meer tijd dan van buiten kennen. Het realistisch rekenen kent veel van dergelijke stappen. Realistische oplossingen bevatten daarom vaak veel meer getallen dan traditionele. Begeleiding moet voorkomen dat leerlingen te omslachtig rekenen.
Realistisch werden ook de opgaven. Rekenen werd minder abstract. In de rekenboeken verschenen minder rijtjes oefensommen met alleen getallen. De opgaven kwamen uit de praktijk: hoeveel kost deze mand vol boodschappen? Wat zijn de gemiddelde kosten per item?
Het realistisch rekenen kwam in de jaren negentig goed op gang. Bij de invoering van de euro in 2002 gingen de basisscholen er massaal toe over. De bestaande boeken die nog met guldens rekenden, waren verouderd, dus er werden nieuwe lesmethodes aangeschaft. De Inspectie van het Onderwijs en onderwijsbegeleiders oefenden druk uit op scholen om tot realistisch rekenen over te gaan. Realistische vaardigheden kwamen in de kerndoelen van het basisonderwijs.
Traditioneel rekenen
Inmiddels is de strijd tussen beide stromingen in het rekenonderwijs aan het wegebben. Bij de nieuwe lesmethodes voor realistisch rekenen is meer aandacht voor oefenen.
De commissie van de Koninklijke Nederlandse Akademie van Wetenschappen zag dat vooral zwakke leerlingen minder baat hebben bij vrije instructie en meer behoefte aan een sturende rol van de leraar. De commissie pleitte voor „meer rust in de presentatie en meer aandacht voor oefenen en het onderhouden van basale vaardigheden en cijferen”.
Daar zijn de voorstanders van realistisch rekenen het nu ook mee eens. Marc van Zanten, verbonden aan het Freudenthal Instituut en aan de Stichting Leerplanontwikkeling (SLO), schreef in een leskatern voor pabostudenten dat het idee „dat oefenen niet meer belangrijk is” soms is „doorgeschoten”. Ook werd soms te weinig gecontroleerd of de zelf bedachte rekenstrategieën van leerlingen effectief waren: „Vooral zwakke rekenaars zien dan door de bomen het bos niet meer.”
Volgens Treffers van het Freudenthal Instituut gebruikt nog wel zeker zo’n 90 procent van de basisscholen een realistische methode. Maar zeker eenderde van de nieuwe schoolbestellingen van nieuwe rekenboeken bestaat uit de methode Getal en ruimte Junior, met rijen traditionele oefensommen met getallen. Ook in de nieuwe realistische rekenboeken zijn meer getallensommen te vinden.
Volgens Van Zanten zegt de keuze van de lesboeken niet alles over het rekenonderwijs op een school: „Er is een verschil tussen oorspronkelijke ideeën, hoe die worden uitgewerkt en wat er in de klas mee gebeurt.” Leraren houden zich vaak niet aan het schoolboek. Als leerlingen de taal van ‘verhaaltjessommen’ niet begrijpen, krijgen ze abstracte opgaven.
Bron: nrc.nl
